BIOL 570 - Lab 1 Sampling and Introduction to R
Goals
- Learn how to make a random sample
- Understand errors vs. biases in both measuring and sampling.
- Learn how to enter data in R, make histograms, and do simple calculations
Introduction
Consult the quick summary of the text for this lab and the Basic intro to R.
Step 1: Log into your computer while your TA introduces the lab.
In today’s lab we will explore the concept of random sampling and learn about the challenges of measurement. Your TA has set out a collection of 200 seashells that w be the “population” for the lab. Each shell has a unique number. Today we will collect the data needed to estimate the mean length of the shells in this population.
Step 2: Choose a partner for today’s lab and introduce yourself.
Each group will choose a random sample of 10 shells from the population. To be random, each shell should have an equal probability of being chosen.
We will use random number
[1] generated by software to choose the shell’s number. We will use the
statistical programming language, R.
Step 3: Open RStudio. Review the basic introduction to R posted the Basic intro to R page, if you have not read it yet.
Step 4: Use R to choose a random number:
sample(1:200, 15, replace=FALSE)
This is a R function call. sample is the name of the function. The information in parentheses are called the arguments to the function. Commas separate the different arguments. The arguments control the behavior of the function. The arguments we are using tell the function the following information:
- The first argument is the population we are sampling from. 1:200 is R shorthand for “a vector of integers [1, 2, 3, … 200].
- The second argument is the sample size. 15 in our case
- replace=FALSE tells the function not to sample the same integer twice.
Note that R (like most programming languages) is case-sensitive. So, it is important to enter the code exactly as written.
Step 5: Execute the code. You can do this by selecting the code and then clicking the green “Run” button (or by pressing both the Control and Enter keys).
Did you see where the output showed up?
Look in the lower output panel. The output from the execution of our code will show up here. You should see something like the following (though your numbers will be different):
[1] 100 62 138 72 147 23 12 200 21 158 31 165 82 107 136
The sample function has randomly selected 15 integers from our population, and returned them as a vector. R is showing you the sample in its output. The [1] at the start of the line is just R’s way of telling you that this row of the output starts with the first element in the returned vector. It is not a member of the sample. If we had asked for a large sample, then R would have displayed the long vector on multiple lines and the prefix for each line would show the index of the first element shown on that line.
Step 6: Write down the 15 random numbers on a slip of paper.
Step 7: Go to the shell population and pick up TEN shells according to the first 10 numbers in your sample that are available (we asked you to generate 15 numbers in case a different group of students is using one of the shells that is in your sample. You don’t need to wait for them to measure the shell, you can just skip to the next number on your list).
Step 8: Fill in your information on your worksheet. The first column of ID numbers should be the number associated with each of the 10 shells that you selected in the previous step.
Step 9: Designate one person as the “measurer” for the day and one person as the “recorder”. The “measurer” should not look at the data sheet until all data have been collected!
Step 10: The measurer should now measure the maximum linear dimension of each shell in centimeters, with one decimal place (ex. 4.5 cm). The “recorder” will write down each of the 10 shell measurements in the column “Trial 1 (my group)”
Step 11: The recorder should fold the sheet so that the measurements from Trial 1 cannot be seen, but the shell IDs can be seen.
Step 12: Now leave your shells and data sheet at your lab location and swap positions with another group.
Step 13: The “measurer” in your group should measure the ten shells from the other group.
The “recorder” in your group should write the measurements in the “Trial 1 (other group)” column).
Step 15: Swap positions with the other group to return to the 10 shells and data sheet you started with. Repeat the measurements, recording them in the “Trial 2 (my group)” column.
Step 14: Finally, swap places with the other group and record the measurements for
“Trial 2 (other group)” column.
Step 15: Store your measurements in a spreadsheet. You can use Microsoft Excel or
Google Sheets (an online spreadsheet. If you use this option, you will need to log in to google with an email account that you have associated with google drive/google docs). Use the first row to enter column headers. It will be easier to deal with these in R if you use short column headers with no spaces in them. So today, you should use the following column headers:
where the shell numbers will go in the Id column, and the other headers coding uses “t” for “trial”, then the trial number, and “m” and “o” for “My Group” and “Other Group” measurements.
It is easiest to enter the data by one person reading to the other (you do not each have to produce a spreadsheet).
Do not put “cm” after the measurements, as that will confuse R.
Step 16. It is easy to calculate the sample means using the AVERAGE function that comes as a part of most spreadsheet software, but we will use RStudio to get used to using R.
Typically, in R we read data from a file, but we can also simply paste the data into a “string” type of variable into our R session, then wrap the string variable using a function that will make it act like a file that holds the data.
We can do this with what is technically 4 lines of R code. Because your data has line breaks in it, after you paste in your data it will be about 4 lines of text.
- copy and paste the following template into your R session:
raw = "YOURDATAGOESHERE"
fakefile = textConnection(raw)
data = read.csv(fakefile, sep="\t", header=TRUE)
print(data)
- In your spreadsheet, select the data (including the header, but not any extra columns or rows)
- Use copy function (Control-C) to put a copy of the data in your computer’s clipboard
- Return to the RStudio window
- Highlight the YOURDATAGOESHERE.
- Paste (Control-V) your data so that it is in between the quotation marks.
Here is what is happening:
- A variable called raw is being created to hold your data as a text (“string” in the lingo of programming).
- A new variable fakefile is created that wraps around the raw variable to make it act like a file with the contents equal to raw.
- Next we use the standard R function read.csv function that is used to read tabular data. By default it reads “comma-separated values” (hence the name csv), but we are telling it that a tab character (encoded as "\t") is the separator used by our spreadsheet. The header=TRUE argument tells the function that the first row consists of column headers, not data. The result is stored in a variable named data.
- Finally we tell R to print out the value of the variable data so that we can check it.
Step 17: Execute the previous code, and make sure that the text that shows up in the output panel makes sense.
Step 18: Note that you can also enter R code in the output panel after the > prompt. Any code put here will be executed as soon as you hit Enter. This can be a nice way to interactively inspect the variables in a session. For example, the data variable that captured the data frame that was returned by the read.csv function can be examined interactively. R uses the dollar sign in a variable name to give you access to one of the vectors (columns of data) inside a data frame. Because, we told the read.csv function to read headers, you can access your first trial’s data with a syntax like:
data$t1m
If you enter that text in the output panel and hit Enter, then you should see just that data show up in the output.
Step 19: R has a function called mean that will calculate the mean of any vector passed in as an argument. To get the mean of the first trial use:
mean(data$t1m)
Execute this code (either by putting it at the end of the code panel and re-executing the code, or by simply typing that in the interactive panel and hitting Enter).
Write down the mean on your worksheet and then use similar syntax to calculate the other three means.
Step 20: Why did we measure these shells so many times? The goal was to learn about four important concepts:
- sampling error: samples will differ from the true population just by chance. The sample means you calculated (
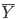 ) will differ from the true population mean (μ). Different samples will also have different sample means. Write the mean from your first column (“Trial 1 – my group”) on the board. As other groups write their numbers on the board, see how much variation there is between numbers. If you were going to repeat this lab and you needed to decrease sampling error, what would you differently?
) will differ from the true population mean (μ). Different samples will also have different sample means. Write the mean from your first column (“Trial 1 – my group”) on the board. As other groups write their numbers on the board, see how much variation there is between numbers. If you were going to repeat this lab and you needed to decrease sampling error, what would you differently?
- sampling bias: Our procedure was randomized, so it should be free of bias. Imagine that we had asked you to choose 10 “typical” shells from the population. This would be very challenging – we might be more likely to notice large shells. Bias is a systematic deviation of the sample from the population.
- measurement error refers to the fact that you will be very unlikely to get the exact same measurement for each shell on your two trials.
- measurement bias: You might have observed bias in which different students systematically measure the same observational units in different way. When you compare your measurements for your shells to the other groups measurements of the same shells, was there evidence of bias?
Measurement error and bias can be reduced by taking more careful measurements. Sampling error is inevitable whenever we cannot sample the entire population.
Histograms are very useful ways to look at the frequency distribution of a data set (i.e. the number of observations
Step 21: Execute the code:
hist(data$t1m, main="Histogram of shell lengths", xlab="Max. Length (cm)")
To generate a histogram of the measurements from trial 1. Note how the second and third arguments control the title of the plot and the label on the x axis. If you right-click on the graph that appears, then you can save the image to your computer. We don’t need to do that now, but it will be useful later in the course.
Step 22: Generate and examine histograms for the other 3 trials.
Step 23: Use a histogram to look at the differences between your first and second measurement of each cell. Because data$t1m is the vector of your first measurements and data$t2m is the vector of the second measurements, the syntax data$t1m - data$t2m will tell R to calculate a vector of differences. Execute the code:
hist(data$t1m - data$t2m, main="Differences",
xlab="Length (cm) from Trial 1 - Trial 2")
And make sure that you understand the syntax and output.
Step 24: That’s it! Turn in your worksheet and return you shells.
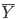 ) will differ from the true population mean (μ). Different samples will also have different sample means. Write the mean from your first column (“Trial 1 – my group”) on the board. As other groups write their numbers on the board, see how much variation there is between numbers. If you were going to repeat this lab and you needed to decrease sampling error, what would you differently?
) will differ from the true population mean (μ). Different samples will also have different sample means. Write the mean from your first column (“Trial 1 – my group”) on the board. As other groups write their numbers on the board, see how much variation there is between numbers. If you were going to repeat this lab and you needed to decrease sampling error, what would you differently?