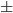 one standard deviation. Recall that the interval between these two values should include roughly 68% of the data.
one standard deviation. Recall that the interval between these two values should include roughly 68% of the data.
BIOL570 Lab 2. Displaying and describing data
Consult the quick summary of the text for this lab.
We will use a small bit of the data collected for this study on the use of antibiotics in hospitals:
Townsend, T. R., et al. "Use of antimicrobial drugs in general hospitals. I. Description of population and definition of methods." Journal of Infectious Diseases 139.6 (1979): 688-697.
https://academic.oup.com/jid/article-abstract/139/6/688/2189681 (also available via JStor: https://www.jstor.org/stable/30109077)
Antibiotic resistance now occurs in high frequency in bacterial populations because antibiotics are so widely used in human medicine, veterinary science, and food production. However, quantifying antibiotic use is difficult.
Step 1. Skim the paper if you have not already done so. Our main goals are for you to understand the structure of a scientific paper and to figure out the what constitutes the sample and population for this study. See what kinds of information are presented in the different sections of the paper (Abstract, Introduction, Materials and Methods, Results, Discussion, References). A couple of notes:
Step 2: As with last week’s lab we are going to simply copy and paste our data into a string in a new RStudio session. There are 7 variables in this study:
Copy the following command in the RStudio code panel and execute the code.
raw = "id,dur.stay,age,sex,temp,wbc,antibiot
1,5,30,F,99,8,N
2,10,73,F,98,5,N
3,6,40,F,99,12,N
4,11,47,F,98.2,4,N
5,5,25,F,98.5,11,N
6,14,82,M,96.8,6,Y
7,30,60,M,99.5,8,Y
8,11,56,F,98.6,7,N
9,17,43,F,98,7,N
10,3,50,M,98,12,N
11,9,59,F,97.6,7,N
12,3,4,M,97.8,3,N
13,8,22,F,99.5,11,Y
14,8,33,F,98.4,14,Y
15,5,20,F,98.4,11,N
16,5,32,M,99,9,N
17,7,36,M,99.2,6,N
18,4,69,M,98,6,N
19,3,47,M,97,5,Y
20,7,22,M,98.2,6,N
21,9,11,M,98.2,10,N
22,11,19,M,98.6,14,Y
23,11,67,F,97.6,4,N
24,9,43,F,98.6,5,N
25,4,41,F,98,5,N"
fakefile = textConnection(raw)
data = read.csv(fakefile, header=TRUE)
print(data)
Step 3: Question 1, write down the six data variables (ignore the “id” variable) and indicate what types of variables they are (ordinal categorical, nominal categorical, discrete numerical, or continuous numerical).
Step 4: Create a histogram of age with the code:
hist(data$age, xlab="Age (years)")
Question 2: Based on the graph, what are your best guesses for the mean, median, first quartile, third quartile, minimum, and maximum values for the variable “age”?
Note that n = 25. You cannot get exact answers by looking at a histogram (because the data are “binned”), but you should be able to get reasonable guesses from the graph.
Question 3: Sketch a box plot that corresponds to your guesses (write numbers on the number line that correspond to your answers from Question 2). Also label the axis (what is the variable being graphed? What are the units for this variable?). (There are no outliers in this data set, so don’t worry about them.)
Step 5: Use R to generate a box plot with:
boxplot(data$age, ylab="Age (years)")
Compare the plot to your sketch from step 4. They should look similar!
Step 6: Create a boxplot of dur.stay variable using:
boxplot(data$dur.stay, ylab="Stay duration (days)")
Recall that the box plot divides the data set into quarters.
Question 4: Fill in the lower and upper endpoints of each quarter of the data for dur.stay in the spaces provided.
Question 5: Is this variable symmetric or skewed? If skewed, make a quick
sketch to show the direction of skewness (no need to write a number line –
just visualize the shape of the data)
Step 7: Create a histogram of dur.stay. Does it generally look like the sketch you drew for Question 5?
Step 8: Now calculate descriptive statistics for age and dur.stay. For age, the commands would be:
quantile(data$age)
mean(data$age)
sd(data$age)
var(data$age)
The quantile command gives the minimum, Q1, median (Q2), Q3, and the maximum. The mean command is self explanatory. sd returns the standard deviation and var returns the variance.
Are the descriptive statistics for age similar to your guesses in Question 2?
When reporting summary statistics, one typically includes a) a measure of location, b) a measure of spread, and c) sample size. We want to practice writing this information in the style you will see in scientific papers.
Question 6. Write a simple sentence that includes your summary statistics for “age”.
Note that you can also get a summary for all of the columns of data with the function:
summary(data$age)
Step 9: Age has a relatively normal distribution. Calculate the two values defining the range: mean age 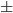 one standard deviation. Recall that the interval between these two values should include roughly 68% of the data.
one standard deviation. Recall that the interval between these two values should include roughly 68% of the data.
Question 7. What % of the actual data set (n = 25) is in this interval? Is your answer roughly what you expected?
R has some interesting syntax for getting subsets of a vector that will help you do this. Normally, R uses an integer in [ ] brackets after a vector name to refer to just that element of the vector. For example, data$age[1] would return the first age in your data set. However, we can also put logical tests in the brackets. In that context, R will return only those elements that match the test or tests. So:
data$age[data$age > 15]
Would return a vector of all ages over 15, and
data$age[data$age > 15 & data$age < 30.1]
would return all ages that were greater than 15, but less than 30.1.
Finally we can use the length function to tell how many entries matched our query. You will need to modify the numbers in this example to use the mean - 1 SD and mean + 1 SD numbers you calculated above, but the following type of syntax should tell you how many data points are inside a range:
length(data$age[data$age > 15 & data$age < 30.1])
Step 10: Now focus on the variable temp.
Question 8. Create a sketch of the cumulative frequency distribution of temp.
You can use:
sort(data$temp)
quantile(data$temp)
to see the data in sorted order, and to see the range and quartiles. That info helps when sketching a CFD graph.
Step 11: Use R to generate this graph using the command:
plot(ecdf(data$temp), xlab="temp (F)", ylab="Cumul. Freq.", verticals=TRUE)
Do you understand why there is a vertical line at 98? Why is there a horizontal line between 97 and 97.6?
Step 12: Question 9: What proportion of the patients received antibiotics?
It is easiest to deal with categorical variable as “tables” in R. So we can call the table function to make a table from a vector, and then ask for the proportions using the prop.table function:
prop.table(table(data$antibiot))
Step 13: High white blood cell counts (wbc) are indicative of infection. One might hypothesize that patients with higher wbc values upon admission to the hospital would have been more likely to be given antibiotics. Is this true?
We can use the trick of putting a logical test in brackets to look at subsets of the data. In this case, to get 2 boxplots of wbc values one figure (one for with antibiotics=Y and the other for no antibiotics), we can use:
boxplot(data$wbc[data$antibiot == "Y"], data$wbc[data$antibiot == "N"], names=c("Y", "N") )
Question 10: Interpret the box plots; in a sentence, state what you infer from the graphs about the relationship between wbc counts at admission to the hospital and the likelihood of being given an antibiotic.