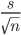Goals

• Learn how to produce a confidence interval from a sample in R
• Understand the relationship between the sampling distribution of an estimate, the standard error, and a confidence interval.

Introduction

From students’ measurements of shells in lab 1, we have compiled 26 samples with n=20. We also have access to measurements from an entire population, so we can assess how accurate our estimates are. The first steps of the lab will produce an interval estimate for a single data set, just as a biologist would do when analyzing his/her data. In the later parts of the lab we will use information from the entire population to demonstrate that the confidence interval is reasonable.

Step 1: Look at the data posted at http://phylo.bio.ku.edu/biostats/Lab3.csv The first column (pop) consists of one length (in cm) for every shell in our population. The next 26 columns (s1, s2, …, s26) are different samples (each with n=20) from this population.

Step 2: Get out your print out of the lab 3 worksheet. Pretend that you only had time to collect twenty measurements and want to infer the population’s mean length. Randomly select one of the twenty-six samples to treat as “your” sample. You can use RStudio to choose a random numbers with:

sample(1:26, 1)

Question #1: What is the number of the sample that you randomly selected?

Step 3: Now you can grab the vector of data for “your” sample using syntax similar to the following (but you should replacing “100” with the random sample number) in the second line :

shells <- read.csv(url("http://phylo.bio.ku.edu/biostats/Lab3.csv"))

d = shells$s100

d = d[!is.na(d)]

Step 4: Recall from previous labs, that we can use

summary(d)

sd(d)

To calculate the summary stats on our vector d (with sd showing you the standard deviation). R also allows other software developers to write packages of code to extend the core language. The package pastecs has a nice summary function called stat.desc. To use it, we have to tell R that we want to load the package:

require(pastecs)

stat.desc(d)

If you see a message which ends in something like “there is no package called ‘pastecs’” then you will need to execute the command

install.packages("pastecs");

And then try the the previous 2 lines again.

Does the standard error of the mean (SE.mean) equal ?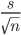

Question #2: Write a sentence that you would put into a scientific publication to describe what you would conclude about the mean length of the population of shells based on your sample of lengths. Remember to include a measure of location, spread, and the sample size.

Step 5: As we discussed in class, the 95% confidence interval for a statistic is a range of plausible values. We say that we are 95% confident that the population parameter value is within our 95% confidence interval. We also noted that when you are estimating the mean of a population from a random sample, then we can use th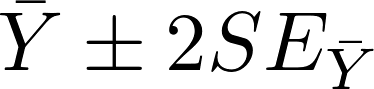e rule as the basis for the confidence interval. The term 2SE is referred to as the "margin of error."   Calculate the confidence interval for the mean for your sample using this 2SE rule-of-thumb. The margin of error will not agree exactly with the CI.mean.0.95 that is shown in the R output; we will learn about how R calculates the margin of error later in the course.

Question #3: Draw a set of axes to plot the confidence interval for your sample. Plot the CI as a line segment above horizontal axis, and add a tick mark to denote the mean.

If you are working the lab in-person, go to the board and plot your CI

Step 6: All of the analyses that we have done to this point in this lab are representative of the steps that you could perform on a typical dataset. Now we are going to do some analyses that exploit the fact that in this (very unusual) case we have access to the entire population. We will compare our estimate of the mean to the true value for the population parameter. Use:

true.val = mean(shells$pop)

pop.sd = sd(shells$pop)

print(paste("true mean = ", true.val, ". sd =", pop.sd))

to examine the parameter values for the entire population (the data in the ‘Length’ column).

Question #4: What are the values of μ (the population mean) and σ (the population standard deviation)? Is μ contained within the confidence interval that you drew on the board?

Step 7: Because we have 26 different samples with n = 20, we can calculate 26 different CIs. First we'll isolate the 26 columns that were random samples, and we'll only keep the first 20 rows of each because there is no data in the later rows. The subset function with a select argument will choose the columns that we want. The logical test “shells$s1 > 0” will trim off the rows with no data. We'll store the result in a data frame called "r"

meanv = 0; sdv = 0;

r = subset(shells, shells$s1>0, select=2:27)

Then to calculate the CI’s, it will be convenient to get a vector of means and standard deviations from each of the 26 random sample. We can do all of that with the following syntax:

for (i in 1:26) {

  samp = r[[i]] ;

  meanv[i] = mean(samp) ;

  sdv[i] = sd(samp) ;

}

Now, given n=20 for each sample, we can calculate a vector of SE for each sample and use the 2 standard errors trick to get a vector of margins of error, and from that the upper and lower values of the CI:

n = 20

se.v = sdv/sqrt(n)

moe.v = 2*se.v

lower.ci.v = meanv - moe.v

upper.ci.v = meanv + moe.v

We can get a vector of T/F values for the cases in which the true value is above the lower limit of the CI and below the upper limit of the CI. sum will count the number of TRUE values, which is the number of CIs that contain the true population mean.

contains.true.val = lower.ci.v < true.val & true.val < upper.ci.v

print(paste(sum(contains.true.val), " of 26 CIs contained the true mean")) 

Question #5: How many of the confidence intervals contain the population mean?

Step 8: As we saw in previous labs, R can randomly sample from a population.

We can put this logic inside a “for” loop to do 200 repetitions of the sampling procedure. Here we’ll generate 200 samples each with n=80. This code may take awhile to execute:

s.contains.true.val = 0

s.mean = 0

s.up = 0

s.lo = 0

s.n = 80

s.se = 0

reps = 1:200

for (i in reps) {

    s.sample = sample(shells$pop, s.n) ;

    ms = mean(s.sample) ;

    s.mean[i] = ms ;

    s.se[i] = sd(s.sample)/sqrt(s.n) ;

    s.up[i] = ms + 2*s.se[i] ;

    s.lo[i] = ms - 2*s.se[i] ;

    s.contains.true.val[i] = s.lo[i] < true.val & true.val < s.up[i]
}

print(paste(sum(s.contains.true.val), " of 200 CIs contained the true mean"))

Step 9: How much variability is there in the estimates of the mean? In the code above, we stored the means from each simulation in a vector called s.mean and we stored the upper and lower values of the CIs in s.lo and s.up vectors. We can make a plot with a point for every replicate’s mean and a CI for every replicate that did not overlap with the population mean using the following code:

plot(reps, s.mean, ylim=c(min(s.lo), max(s.up)), ylab="mean", xlab="rep. #")

segments(reps, s.lo, reps, s.up, col="grey", lty=2)

To plot each mean against its replicate number and show the confidence interval as a grey, dashed line. Because s.contains.true.val is a vector that stores TRUE or FALSE depending on whether or not each replicate's CI contains the true value, we can identify the replicates that exclude the true value as the TRUE values in an excl vector, and then plot those CIs in red.

excl = !s.contains.true.val

segments(reps[excl], s.lo[excl], reps[excl], s.up[excl], col="red")

Finally can add a horizontal line corresponding to the true value across our plot:

abline(h=true.val)

Recall the the sd functions will report the standard deviation for a vector.

Question #6: Based on the 200 sample means we have drawn and stored in s.mean, what is the standard error of the mean for a sample size of 80 shells drawn from our population?

Note that, in question 6 you are not reporting the standard error; you are reporting

an estimate of the standard error.

Step 10: Usually we estimate the standard error of the mean for a single sample, using the formula 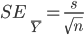. The estimates of the standard errors are stored in the vector s.se. If you print out that vector, are the estimates similar to the value you calculated for question 6?

Step 11: Use the print(s.mean[1]), print(s.lo[1]) and print(s.up[1]) functions to see the limits of the first simulated 95% confidence interval that you create for n=80. Go to the board and draw a line below the number line to depict that confidence interval

interval for this sample; add a tick mark to denote the mean.

Question #7: Look at the confidence intervals drawn on the board. Which sampling scheme (n = 20 or n = 80) results in a tighter confidence interval? Do the results reflect what you expected to see?

Remember: a 95% confidence interval for a larger sample size should encompass a smaller

range (the interval should be tighter) than the 95% confidence interval based on a small

sample size. In the long run, 95% of all 95% confidence intervals should contain the

population mean – whether the sample size is small or large. Better sampling shrinks our

confidence interval, it does not increase the chance that the interval contains the population

parmeter value!