Goals

• Understand how the chi-square goodness-of-fit test can be applied to several different kinds of research questions
• Learn how to do a chi-square goodness-of-fit test using R

Introduction

The chi-square goodness-of-fit test can be used when the null hypothesis makes specific predictions about the population proportions of the different values of a categorical variable. There are several different “probability models” that can be used to generate these proportions. These include a) the proportional model, b) models generated by scientific hypotheses or theory, and c) discrete 1 probability distribution models.

As usual, we will assume alpha = 0.05 for all tests.

Part 1: Proportional null models

In a proportional model, the expected proportions of occurrences is proportional to the number of opportunities.

Example: Imagine you are examining a data set of weights and you are trying to assess whether the data were obtained through actual measurements as opposed to “self-reporting”. One approach is to analyze the “last digits” of weights. With “self-reporting”, people tend to report more 0’s or 5’s than one would expect in an actual measurement. In contrast, if people are actually weighed, all last digits (0,1, 2...9) should occur with roughly equal frequencies.

First state the null and alternative hypotheses. These hypotheses can be stated in terms of proportions or probabilities. Remember that the hypotheses always refer to the population, not the sample. For example,

H0: The probabilities of a weight with a last digit of 0 through 9 are all equal to each other.

HA : At least one of the probabilities is different from the others.

Step 1: Execute the following command in RStudio

last.digits = c(5, 8, 4, 0, 0, 5, 0, 3, 4, 0, 0, 9, 5, 5, 8, 0, 0, 0, 5, 0,

                8, 5, 7, 0, 0, 5, 0, 5, 4, 0, 0, 5, 0, 7, 0, 5, 7, 0, 0, 0,

                5, 5, 5, 5, 0, 5, 5, 0, 5, 0, 5, 1, 9, 4, 0, 0, 0, 0, 2, 5,

                0, 5, 0, 0, 7, 5, 8, 8, 8, 0, 5, 0, 8, 0, 0, 0, 5, 5, 6, 0);

To set the variable last.digits to hold a vector of the last digit of the self-reported weight (in pounds) of 80 people. Examine the data. Does it appear that there are more 0’s and 5’s than you would expect under the null hypothesis?

Step 2: To visualize the data use:

hist(last.digits);

ldt = table(last.digits);

print("In tabular form:"); print(ldt);

The result of printing the table ldt is a frequency table with two rows of numbers.

Question 1. How many variables are represented in the frequency table?

Step 3: There appears to be an excess of 0’s and 5’s in the data, but we need to figure out the expected numbers.

Question 2. If the null hypothesis were true, what are the expected numbers for each of the 10 digits for a study with n=80?

We can check your answer with R:

n = length(last.digits) ;

expected.prop = 1/10 ;

expected.n = rep(n*expected.prop, 10) ;

print("The expected numbers are: "); print(expected.n);

Step 4: A grouped bar chart is a convenient way to display observed and expected values. To generate this plot, we will first extract the data from the ldt frequency table as a vector of numbers, and then group the observed and expected numbers together with the function rbind:

observed.n = as.vector(ldt) ;

grouped = rbind(observed.n, expected.n) ;

barplot(grouped, beside=T, names.arg=0:9, ylab="number", xlab="last digit") ;

Step 5: To conduct a chi-squared test, we need to calculate the sum of 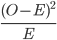 for each category.

Question 3. Calculating the term for the “0” last digit category “manually”.

To check your answer with R, use:

chi.sq.terms = ((observed.n - expected.n)^2) / expected.n ;

print("The terms of the chi-sq test statistic are:") ; print(chi.sq.terms) ;

where the ^2 syntax is how we square a number in R.

Step 6: Recall that the chi-squared test statistic is the sum of these terms over all categories:

chi.sq = sum(chi.sq.terms) ;

print("The test stat =") ; print(chi.sq) ;

Step 7: In class, we are using a chi-squared table to bound the P-value, but computers can give us very accurate approximations of the P-value. First we need to know how many degrees of freedom there are in this chi-squared null distribution.

Question 4. What is the degrees of freedom for our test?

Set a variable df in your R session to hold this integer, then execute the following:

p.val = pchisq(chi.sq, df=df, lower.tail=F) ;

print("The approx. P-value = "); print(p.val) ;

Chi-squared goodness-of-fit tests are pretty common, so we could have asked R to do the test in a more automated way:

chisq.test(x=observed.n, p=expected.n/n) ;

Where the p argument is the expected proportion in each category (in the line above, we get this by dividing the expected number by the sample size).  You should get the same test statistic (though the approximate P-value may be reported in a different way).

Question 5. Summarize your results for this problem in the same “style” we have used in lecture. Make sure to include the sample size, test statistic, P-value, and df. It would be cumbersome to list the descriptive statistics (i.e. effectively the count data from each category), so no need to do this – in a paper you’d likely produce a graph. However, do make sure that your results provide a sense of the data (i.e. if they deviate from the Ho, what is the pattern of the deviation?)

Part 2: Null models generated by a specific hypothesis or theory

Problem: Genetic counselors that work with pregnant women at high risk of fetal disorders hypothesize that about one-half of all disorders are trisomy 21, one-third are trisomy 18, and the remainder are trisomy 13 (trisomy refers to three copies of a particular chromosome). To test this hypothesis, a sample of 200 pregnant women who deliver babies with chromosomal disorders are studied. The data are:

Question 6. State the null and alternative hypotheses for a goodness of fit test.

Question 7. What are the expected numbers for each category?

Step 8: Execute the one-line version of the test in R:

chisq.test(x=c(107, 70, 23), p=c(.5, 1.0/3, 1.0/6)) ;

Question 8. State your conclusions.

Part 3: Null models from discrete probability distributions

If the assumptions of the null model fits the assumptions of a standard discrete probability model, we can use that probability distributions.

Problem: At a university, incoming students are assigned to an orientation seminar class of 7 students. The university reports population stats of 60% women and 40% men. Jose happens to be in a class with six men and one woman, and he wonders how the students were assigned to specific classes. He obtains data on the sex ratio of the classes for the whole university (1000 total classes had exactly 7 students). He explores if they data are consistent with the university assigning students to seminars in a manner that is random with respect to sex of the students:

H0: Students are assigned randomly to the seminar, so the sex ratio reported for the seminars should fit the binomial distribution with p0=.6. (where “woman” defined as “success” for the purpose of this test).

HA: The sex ratio of the seminars does not fit this binomial distribution.

Question 9: What are n and p for the binomial that will give us the null expectations? Comment on whether the null matches the four requirements of binomial mode:  (1) 2 outcomes per trial ^[1] ; (2) fixed n;  (3) fixed p; (4) the n trials are independent.

Step 9: Execute the following code block in R. As with previous labs, this mimics read the data from a file into a data frame called s. Then it creates a barplot of the data.

raw = "n.women,n.classes

0,5

1,15

2,81

3,180

4,288

5,259

6,133

7,39" ;

fakefile = textConnection(raw) ;

s = read.csv(fakefile, sep=",", header=TRUE) ;

barplot(s$n.classes, names.arg = s$n.women, ylab="# of classes") ;

To test the null hypothesis with a chi-squared test, we need to figure out the expected numbers of each type of class if students were assigned randomly to classes and p0=0.6.

Question 10: Use the binomial formula (which we covered last week) to calculate the number of classes out of 1000 that one would expect to be like Jose’s (six men and one woman), given the null hypothesis. Show your work.

Step 10: Recall from last week’s lab, that we can calculate the probabilities for the entire domain of the binomial distribution with one line:

expected.class.p = dbinom(0:7, size=7, p=0.6);

expected.class.n = 1000*expected.class.p ;

print("The expected numbers in each category are:"); print(expected.class.n);

Remember that there are rules about whether the expected numbers are large enough to allow us to use a chi-squared test without grouping categories. Do any of the categories have expected numbers < 1? Do more than 20% of the categories have expected values < 5?

Step 11: Now we can conduct the hypothesis test using:

chisq.test(x=s$n.classes, p=expected.class.p) ;

You will probably see “Chi-squared approximation may be incorrect” warning, because R uses rules about the expected values that are stricter than the ones we use in this class. It is fine to ignore this warning in today’s lab.

Optional: If you would like to see a plot of the observed and expected numbers, see footnote [2]

Question 11. State your conclusion (recall that we need a test statistic, df, P-value, and sample size). Don’t worry about including descriptive statistics; for this test, you would more likely provide a graph for illustration

Imagine that you had a sample of 4000 classes (instead of 1000), but the same observed proportions.  This is easy to do in R:

chisq.test(x=s$n.classes*4, p=expected.class.p) ;

Would your conclusions have been the same?

Optional Step 12: Below are some more examples of the chi-square test for you to practice with on R. We strongly encourage you to work through as many of these as you can during this laboratory session, when you can ask your TA for help.

We can use the chi-square test when our data consists of counts for a categorical variable from independent samples and we are testing a null about the expected proportions of outcomes for each category.

As with all tests that we cover in this course, the test works by quantifying whether the sample data are consistent with the null. If so, we should “not reject the null hypothesis”. Alternatively, a high value of the test statistic means that there is low probability of seeing data this unexpected if the null were true.  If the P-value is smaller or equal than alpha, we will reject the null hypothesis; if the opposite is true, we would ‘not reject” the null hypothesis. Ask your TA if you are uncertain about how to apply the chi-square test to each of these problems.

For each problem below, make sure that you can state the null and alternative hypotheses, determine your test statistic, df, and P-value, and state your results.

Example 1: Volunteers at a teen hotline in a local community have been trained based on a national survey that found that 40% of calls are drug related, 25% are sex related, 25% are stress related, and 10% concern educational issues. To test whether this pattern holds in this particular community, data were collected from 120 randomly selected calls placed to the teen hotline (each call was classified into one of these categories based on the primary issue raised by the caller). The data in an R data frame are:

calls = data.frame(issue=c("drug", "sex", "stress", "education"),

                   counts=c(34, 30, 26, 30));

Example 2: The number of accidents in a factory during the months of a year is as follows: January = 26, February = 28, March = 24, April = 18, May = 17, June = 27, July = 9, August = 18, September = 22, October = 14, November = 12, and December = 26.

Does the number of accidents depend on the month of the year?

Example 3: The number of eggs laid by a species of bird is three. Overall, the probability that an egg will successfully hatch is thought to be 0.55. A researcher examines 86 nests and records how many fit each possible category. Her categories and data are as follows:

She is curious if her data are consistent with independent fates of each egg, and thus asks whether her data fit a binomial distribution.

Example 4: A cross between white and yellow summer squash given progeny of the following colors: 120 white, 40 yellow, and 17 green. Are these data consistent with a 12:3:1 ratio predicted by a genetic model?