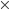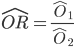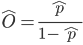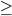Goals

• Learn how to do a chi-square contingency tests in R, including practicing the steps in hypothesis testing.
• Learn how data are typically recorded in a study, and how to convert such raw data into contingency tables.
• Practice working with odds ratios

Introduction

The chi-square contingency test is an important way to evaluate whether two variables are independent of each other. The simplest case is a  table. The test can be extended, however, to any number of rows and columns. As usual, we will assume alpha = 0.05 for all tests. For situations with only two variables and two outcomes per variable, we can also use the odds ratio to summarize the magnitude of the association between the variables.

PART 1: contingency tests

Let’s consider an actual study (Govind, C. K., and Joanne Pearce. "Differential reflex activity determines claw and closer muscle asymmetry in developing lobsters." Science 233 (1986): 354-357.).

Problem 1 The two claws of juvenile lobsters are identical. By adulthood, however, typically the two claws have differentiated into a stout claw called a “crusher” and a slender claw called a “cutter”. A research team wanted to determine the effect of the environment on the differentiation process. They took juvenile lobsters and placed them in one of three experimental treatments: 26 were reared in smooth plastic trays, 18 were reared in trays with many oyster chips (i.e. broken shells) which allowed the animals to exercise their claws, and 23 were reared in trays with only one oyster chip.

The claw configurations of individual lobsters were then scored as adults:

Did the rearing environment affect the development of the lobster claws?

Question 1: State the null and alternative hypotheses.

Question 2: What is the expected number of animals with two cutter claws in the smooth plastic treatment if the null hypothesis is true? (Show your calculations/work.)

Question 3. What are the degrees of freedom for this contingency test?

Step 1: For a tiny data table like this, it is quite easy to just create the data by hand. First by creating a vector by reading the top row, the middle row, and then the last row. Then we can tell R that the data should be shaped as a 3 x 3 matrix. Open RStudio and execute the following code:

data.vec = c(2, 4, 20, 8, 9, 1, 7, 9, 7) ;

observed = matrix(data.vec, 3, 3, byrow=TRUE) ;

print("The observations were:"); print(observed);

Step 2: Recall that the next step in a contingency test is calculating what we would expect if the null were true. The null is that the treatment variable (quantity of oyster shells) is independent of the response variable (claw type). Under independence, for any i and j, we have:

Pr(outcome in row i and column j ) = Pr(outcome in row i ) Pr(outcome in col j )

And the expected number (rather than the probability) under independence is:

 E(row i and column j ) = n 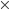Pr(outcome in row i ) Pr(outcome in col j )

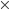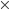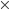                                                  = nPr(outcome in row i ) n Pr(outcome in col j ) / n

       = (row i sum)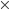(col j sum) / n

So we need to calculate the row, column and grand sum (n). Execute the following:

row.sum = c() ;

col.sum = c() ;

for (i in 1:3) {

  row.sum[i] = sum(observed[i,]) ;

  col.sum[i] = sum(observed[,i]) ;

}

print("The row sums are:"); print(row.sum) ;

print("The column sums are:"); print(col.sum) ;

grand.sum = sum(row.sum)

print("The grand sum is:"); print(grand.sum) ;

This relies R subscripting tricks: m[1,] is the first row of matrix m, and m[,1] is the first column. In the code snippet we use a for loop which does the same operations for i=1, i=2, then i=3.

The clearest way to construct the matrix of expected number is probably:

expected = matrix(nrow = 3, ncol=3)

for (i in 1:3) {

  for (j in 1:3) {

    expected[i,j] = row.sum[i] * col.sum[j] / grand.sum ;

  }

}

print("The expected number are:"); print(expected);

Are the expected numbers large enough to allow us to use the chi-squared test?

Question 4 Use the expected numbers and the observed data to manually calculate the chi-squared term that is contributed by the cell for “no oyster chips” and “both cutters”.

Now let’s check your answer.

Step 3: Because R operates on vectors and matrices cell by cell, producing the chi-square terms of the test-statistic:

c2terms = ((observed - expected)^2)/expected

print("The terms of the chi-sq test stat are:"); print(c2terms);

c2 = sum(c2terms)

print("The chi-sq test stat is:"); print(c2);

Did your manual calculation agree with the relevant cell in the c2terms matrix?

Now that we have the test-statistic, we can calculate P-value. First you’ll need to set a variable df in your R session to hold the degrees of freedom for the test, then execute the following:

p.val = pchisq(c2, df=df, lower.tail=F) ;

print("The approx. P-value = "); print(p.val) ;

R will actually conduct the full test from a matrix of counts, so you can verify your work by simply executing:

chisq.test(observed) ;

Note that if you run:

result = chisq.test(observed) ;

you will not see the results of the test. Instead, you have captured the list of results returned by the function in a variable called "result".
If you square the residuals object inside the result list then you should see the chi-squared contributions that you calculated above:

(result$residuals)**2 ;

Question 5. Interpret the results of this study, and write a complete statement of the conclusion. Make sure to include your sample size (n), test statistic, degrees of freedom, and P-value.

Question 6. If one reads the original study, each lobster was raised in its own box. This was partly done because lobsters can be aggressive with each other. However, it also was a good statistical practice. What statistical problem was avoided by this approach (hint: this is a subject of one of Whitlock’s “interleafs”)?

Problem 2. Levitt (2005) studied the consequences of car accidents for children ages 2-6 years who were involved in an accident severe enough that at least one other person was killed. Individual children were scored as either being in a car seat, with lap and shoulder belts, or lap belts alone.

Step 4: You can see the data at http://phylo.bio.ku.edu/biostats/Lab8restraints.csv  to read it into R we'll use:

dat <- read.csv(url("http://phylo.bio.ku.edu/biostats/Lab8restraints.csv"));

It takes a few moments to load. The file excludes data on children who were wearing no restraint (the data are very clear that using no restraint at all is much more dangerous than the other options). We are giving you the “raw data” for this file, which consists of 16529 rows of data! Note that using a row for each observation, with columns for variables, is a very common approach for large data sets.  You can get a summary to the data with:

summary(dat) ;

Question 7. State the null and alternative hypotheses for this problem.

Step 5: To perform a test, we need to convert the data frame called data (which has 16529 rows of data)

into a tabular representation. We don’t want the ID field of the data frame in our table (that is not data, just an identifier for each observational unit in the study). Then we can run the chi-squared contingency test on that table:

dt = table(dat$restraint, dat$status) ;

print("The observed counts are:") ; print(dt) ;

chisq.test(dt) ;

Question 8. Write out the contingency table on your study sheet (make sure to label your rows and columns and include the row and column totals).

Question 9:Use the result = chisq.test(dt); print(result$residuals**2) trick to see the contributions to the chi-square. Which combination of “restraint” and “status” has the largest “contribution to the Chi Square”? Interpret this information: what does the results of this “cell” tell you about child safety?

Question 10: Interpret the results of this study, and make sure to include your sample size (n), test statistic, degrees of freedom, and P-value. Make sure you explain major patterns in the data.

Part 2: Odds ratios

Next we will analyze a subset of the data using the odds ratio approach. The odds ratio approach can only be done with two variables, each with two possible outcomes. We’ll focus on the first and third rows of your table: having a car seat versus only a lap belt.

The equation for the estimate for the odds ratio is: 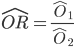 but in order to use this we have to decide what treatment is group 1 and what treatment is group 2. The decision is arbitrary, but we have to remember what we decide because it controls the interpretation of the odds ratio. We will define group 1 as the “car seat” group and group 2 as the “lap belts alone” group.

An odds is the ratio of the probability of an event occurring over the probability of it not occurring:
So, we also have to decide what probabilistic event we are calculating the odds for. If we want to know “what is the odds of an accident resulting in a serious injury”, then we should p̂ is defined as the proportion of children of the appropriate category who had “serious” injury. Use a calculator to determine each of these two odds, and then divide them to generate the odds ratio.

Question 11. List the odds of serious injury given a child seat, the odds of serious injury given a lap belt, and the odds ratio.

Question 12. Calculate a 95% confidence interval for the odds ratio. What does this tell you about the study? Is it consistent with your answer to question 9?

Optional practice problems

We strongly encourage you to work through as many of these as you can during this laboratory session, when you can ask your TA for help.

In a chi-square contingency test problem, you are focusing on two categorical variables (ex. restraint type and injury status of child). Each variable can have two or more outcomes or possibilities. The data for a contingency test can be arranged in a contingency table.

The null hypothesis is that the two variables are independent of each other. We compare the observed numbers in the contingency table to expected numbers that would occur if the null hypothesis were true using the chi-square test statistic. The degrees of freedom for significance testing is calculated using as (r – 1)(k – 1). As always, if the P- value is smaller or equal than alpha, we will reject the null hypothesis; if the opposite is true, we would ‘not reject” the null hypothesis. For each problem below, make sure that you can state the null and alternative hypotheses, determine your test statistic, df, and P-value, and state your results.

Example 1: The Census Bureau collects data on years of school completed by Americans of different ages. The following is a subset of the Bureau’s extensive database:

Does knowledge of a person’s age tell you anything about their likely educational experience?

Example 2: A marketing research firm mailed a questionnaire to small, medium-sized, and large companies. 18 of the small companies responded while 12 did not. For the medium companies, 14 responded and 15 did not. 12 of the large companies responded and 18 did not. Does the size of the company affect whether it responds to a questionnaire?

Example 3: PTC is a compound that has a strong bitter taste for some people and is tasteless for others. The ability to taste this compound is an inherited trait. A researcher was curious whether the proportion of people who taste PTC varies among countries. In a survey, there were 56 tasters and 23 nontasters in Ireland. In Portugal there were 35 tasters and 109 nontasters while in Norway, the number of tasters was 35 and the number of nontasters was 18. What should the researcher conclude?