BIOL570 Lab 10: t-tests comparing the means between groups.
For the first part of the lab, we are going to examine some data on whether or not mosquitoes preferentially bite people who have malaria (which is transmitted by mosquitoes). Researchers conducted a series of trials in which a patient with malaria and two uninfected people were put in a controlled environment. Then the researchers released a mosquito and measured which person attracted the mosquito first.
Our data set is from a series of 100 tests (each with a different mosquito). The number of mosquitoes attracted to the patient with malaria was recorded as the “before” value. Next, the patient was treated for malaria. When the patient was no longer showing symptoms of the disease, the experiment was repeated using the same three people. In this “after'' treatment none of the three people showed signs of having malaria. Once again, the preferences of 100 mosquitoes were tested, and the number of mosquitoes that were attracted to the patient that had been treated for malaria was recorded as the “after'' measurement.
A pair of “before” and “after” measurements constitutes a single trial. These measurements represent a natural pairing because they record the number of mosquitoes that a particular person attracted, and the only factor that varies between the measurements is whether the person was showing symptoms of malaria (the “before'' measurement) or not (the “after'' measurement). To control for the fact that different people may be more or less attractive to mosquitoes (regardless of the person's malarial status), a total of twelve patients with malaria were examined in this way.
Question 1. What are the appropriate null and alternative hypotheses for this experiment?
Step 1: Get the data into RStudio:
raw = "group,before,after
A,19,40
B,77,8
C,11,50
D,28,40
E,42,0
F,85,7
G,90,23
H,12,18
I,78,14
J,50,25
K,62,9
L,50,41"
fakefile = textConnection(raw)
data = read.csv(fakefile, header=TRUE)
print(data)
Step 2: Make a difference in the change in the number of mosquitoes attracted by executing:
hist(data$before - data$after, xlab="Change in # of mosquitoes (before - after)") ;
Use a histogram to get a sense of how the magnitude of differences between the number of mosquitoes attracted to a person when the person had malaria and the number attracted when the person does not have malaria.
Question 2. If we find evidence that the difference is a positive number, what will our biological conclusion be?
Based on visual inspection, do you think that there will be a significant evidence to reject the null hypothesis that the infection status of a person does not affect his/her attractiveness to mosquitoes? (It is OK if this is a guess, just think a bit about whether the data seem to be clear about whether or not there is an effect of infection status.)
Step 3: We are interested in whether the difference between the before-treatment and after-treatment data is significantly different from 0. Because we have a pair of measurements that are naturally linked to each other (they come from trials that involved the same group of three people), this problem is an example of a paired t-test. Recall that when we do a paired t-test, we are effectively just doing a one-sample t-test on the difference between each member of the pair. So we will use the same type of R command that we used last week:
t.test(data$before - data$after, mu=0) ;
Question 3. What do you conclude about whether or not malaria infection makes a person more attractive to mosquitoes?
Note that you can also conduct the test by passing in both vectors (rather than a vector of differences) by using:
t.test(data$before, data$after, mu=0, paired=TRUE) ;
Question 4: Did you get the same result when you performed the paired t-test this way?
Step 4: For a paired t-test, it can be convenient to look at a scatterplot of the pairs of measurements with the equality line plotted:
axr = c(0, max(c(data$before, data$after)))
plot(data$before, data$after, xlab="before", ylab="after", xlim=axr, ylim=axr);
abline(0, 1);
The axr line is creating a vector with 0 and the largest value in the dataset. We use the xlim and ylim arguments to tell R to plot this range along both axes. The abline function takes the y-intercept (0) and slope(1) of a line to overlay on the plot.
Maguire et al. (2000) studied whether obtaining spatial knowledge changes in people's brains:
“Taxi drivers in London must undergo extensive training, learning how to navigate between thousands of places in the city. This training is colloquially known as ‘being on The Knowledge’ and takes about 2 years to acquire on average. To be licensed to operate, it is necessary to pass a very stringent set of police examinations. London taxi drivers are therefore ideally suited for the study of spatial navigation.”
The hippocampus is a region of the brain that is known to have a role in facilitating spatial memory. In particular, the posterior region of the hippocampus has been hypothesized to be associated with spatial memory. Maguire et al. (2000) compared the size of the hippocampus in people who had been taxi drivers for a long time (and presumably had acquired a large amount of spatial information), versus those who have just become taxi drivers (and presumably have not yet learned all of the spatial information). The size of brain regions of taxi drivers was measured using MRI.
Ideally, we would analyze this data in the form of a test of the relationship between two continuous, numerical variables - we would compare the length of time someone has been a taxi driver to the size of that person's hippocampus. We have not covered the statistical methods for such an analysis yet. For today's lab, we will “bin” the amount of time that someone has been a taxi driver into two groups: those who have been taxi drivers less than 15 years, and those who have been taxi drivers for at least 15 years. This creates two populations of subjects for the study. Maguire et al. (2000) were interested in whether the aspects of the brain differ between these groups.
Step 5: Get the data in R’s memory by executing:
raw = "months.driving,post.hippo.diff,ant.hippo
54,-2.4,110.68
60,0.35,97.55
62,-0.44,95.85
67,-3.53,114.55
72,-1.68,90.29
90,-4.05,115.63
102,-1.33,114.08
139,-4.77,111.77
223,-3.88,71.59
258,0,103.58
258,-2.2,71.59
272,0.07,84.26
272,1.41,69.89
340,3.09,85.96
349,3.98,96.93" ;
fakefile = textConnection(raw) ;
data = read.csv(fakefile, header=TRUE) ;
print(data) ;
Question 5. What are the appropriate null and alternative hypotheses?
Step 6: The first column of the worksheet is the number of months that the subject has been a taxi driver. The next two columns are measurements of the volume of the hippocampus. The post.hippo.diff column is the difference between the volume of the posterior part of the hippocampus (in mm3) minus the average volume of that part of the brain in a person of the same age. Larger numbers correspond to larger posterior portions of the hippocampus; negative numbers indicate smaller than average posterior hippocampus).
The measurements for the anterior portion did not require age-standardization, so that data (in the ant.hippo column) are actually the volume of that region.
Question 6. Are these data paired (can we use a paired t-test)?
Step 7: Let’s see if there is any hint of a relationship between the amount of time as a taxi driver and the post.hippo.diff to make scatterplot:
plot(data$months.driving, data$post.hippo.diff,
xlab="months as taxi driver",
ylab="Posterior hippocampus difference.") ;
Because the researchers believe that experience as a taxi driver causes the hippocampus to change, we put the months spent as a driver on the X-axis (explanatory variable) and the posterior hippocampus volume on the Y-axis (response variable). Later in the course, we will discuss how to compare two continuous variables (like the brain volume measurements and the number of months). For now, we will bin the data into groups those subjects who have been taxi drivers for 15 years (180 months) vs those who have been driving taxis for at least 180 months. First lets create two variables to hold the posterior hippocampus data for the two groups (lt for the <15 years group, and geq for the >15 years group):
lt = data$post.hippo.diff[data$months.driving < 180] ;
geq = data$post.hippo.diff[data$months.driving >= 180] ;
We can visualize the differences between the groups using a pair of boxplots:
boxplot(lt, geq, names = c("<15 yrs", ">= 15 yrs"), ylab="post.hippo.diff") ;
Question 7. Based on the boxplots, do you think that we will find a significant difference in the size of the hippocampus between those drivers with < 15 years experience and those with > 15 years experience?
Step 8: Let’s take a look at some summary stats:
require(pastecs) ;
stat.desc(lt) ;
stat.desc(geq) ;
If you see a message which ends in something like “here is no package called ‘pastecs’” then you will need to execute the command
install.packages("pastecs");
And then try the the previous 3 lines again.
Question 8: Use the summary statistics that you displayed to calculate a t-statistic for the difference in means for the posterior hippocampus (comparing the difference to an expected value under the null of zero). What is the value of the t-statistic?
Recall that:
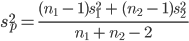
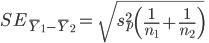
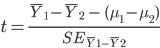
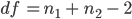
Question 9. Set a variable called df to hold the correct degrees of freedom and use:
pt(0.975, df=df)
to find the critical value.
Question 10. Which population mean did you subtract in order to calculate the t-statistic? If you were to get a positive value for the difference in means, what would this indicate biologically? (Would it appear that taxi driving increased or decreased the size of the posterior hippocampus?)
Step 8: Recall that, in this course we are not going to worry about the Welch's t-test (which does not assume equal variances). So to check your work in R, use the version of the t-test that assumes that the variances in the 2 populations are equal:
t.test(lt, geq, var.equal = TRUE);
Question 11: What is the P-value reported by R? Make sure that the t-statistic agrees with the one you calculated for Question #8.
Question 12. What should we conclude from this study?
Step 9: Do the data appear to fit the assumptions of normality? Execute the commands:
qqnorm(lt) ;
qqnorm(geq) ;
You'll see a plot similar to the normal quantile plot that we discussed in lecture. R puts the quantiles from your data on the y-axis and the quantiles of the standard normal on the x-axis. Does the plot appear to be approximately linear?
These data are not obviously non-normal, so we would usually just conduct the t- test as we have just done above. If normality tests had shown strong deviations from normality, then transforming the data or using a non-parametric tests (such as the Mann-Whitney U-test) would be recommended.
Step 10: Now, following the same procedure as above, use R to perform a two-sample t-test for the anterior portion of the hippocampus.
Question 13. Are the results similar to what was found earlier for the posterior hippocampus? What is the P-value for this comparison?
References: Maguire, Eleanor A., et al. "Navigation-related structural change in the hippocampi of taxi drivers." Proceedings of the National Academy of Sciences 97.8 (2000): 4398-4403.