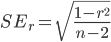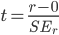BIOL570 Lab 12: Correlation and regression
Goals
- Learn how to plot the relationship between two numerical values using R.
- Learn how to carry out regression analysis and test of correlation using R.
Introduction
We will once again be using the study by Maguire et al. (2000). That study compared the size of the hippocampus in people who had been taxi drivers in London for a long time (and presumably had acquired a large amount of spatial information), versus those who have just become taxi drivers (and presumably have not yet learned all of the spatial information). The size of brain regions of taxi drivers was measured using MRI. The hippocampus is a region of the brain that is known to have a role in facilitating spatial memory. In particular, the posterior region of the hippocampus has been hypothesized to be associated with spatial memory.
In a previous lab, we “binned” the amount of time that someone has been a taxi driver into two groups: those who have been taxi drivers less than 15 years, and those who have been taxi drivers for at least 15 years. This allowed us to create two populations of subjects for our study, and let us carry out t-tests.
In today’s lab, we will analyze this data in the form of a test of the relationship between two continuous, numerical variables -- we will consider the relationship between the length of time someone has been a taxi driver and the size of that person's hippocampus. The first step is taken directly from the previous lab:
Part 1. Linear regression
Step 1: Get the data into an RStudio session:
raw = "months.driving,post.hippo.diff,ant.hippo
54,-2.4,110.68
60,0.35,97.55
62,-0.44,95.85
67,-3.53,114.55
72,-1.68,90.29
90,-4.05,115.63
102,-1.33,114.08
139,-4.77,111.77
223,-3.88,71.59
258,0,103.58
258,-2.2,71.59
272,0.07,84.26
272,1.41,69.89
340,3.09,85.96
349,3.98,96.93" ;
fakefile = textConnection(raw) ;
data = read.csv(fakefile, header=TRUE) ;
print(data) ;
The first column of the worksheet is the number of months that the subject has been a taxi driver. The next two columns are measurements of the volume of the hippocampus. The post.hippo.diff column is the difference between the volume of the posterior part of the hippocampus (in mm3) minus the average volume of that part of the brain in a person of the same age. Larger numbers correspond to larger posterior portions of the hippocampus; negative numbers indicate smaller than average posterior hippocampus).
The measurements for the anterior portion did not require age-standardization, so that data (in the ant.hippo column) are actually the volume of that region.
Step 2: First, we will visualize the data graphically with a scatterplot. Use:
plot(data$months.driving, data$post.hippo.diff,
xlab="months as taxi driver",
ylab="Posterior hippocampus deviation (cubic mm)");
to look at the relationship between number of months driving and the size of the posterior hippocampus. We are putting months spent as taxi driver on the x-axis because it is the explanatory variable, and posterior hippocampus volume on the y-axis because it is the response variable
Question 1. Based on the scatterplot, do you think that we will find a significant linear relationship between the size of the posterior hippocampus and the number of months spent as a taxi driver? Is the relationship positive or negative?
Step 3: Next, we will use R to carry out a linear regression of the posterior hippocampus volume on months as taxi driver. The R function lm constructs a linear model. We specify the model using the syntax of: response variable name, a tilde, then the explanatory variable names. Finally we pass in the data frame (data in our example) that holds those variables. So our command should be:
lin.mod = lm(post.hippo.diff ~ months.driving, data=data) ;
print(lin.mod) ;
This should show the us the estimates of the y-intercept and slope of the regression line.
Step 4: Put the regression line onto the scatterplot by executing the following code with the words “yintercept” and “slope” replaced by the estimates reported by the lm function:
abline(yintercept, slope);
Does the line appear to be the best linear model for the data? (it should pass through the cloud of points in a way that minimizes the distance from the points to the line).
Question 2: Write out the prediction equation. What is the point estimate of the slope? What is the point estimate of the y-intercept?
Step 5: In addition to estimating the regression line, R has done t-tests of both the hypothesis that y-intercept (α) is 0 and the hypothesis that the regression slope (β) is 0. We can see these results of this test by executing:
summary(lin.mod) ;
Recall that, just as ANOVA (and an F-test) can be used to compare two population means instead of a two-sample t-test, ANOVA can be used to test for a significant slope in place of the t-test of the regression slope. The resulting P-values are equivalent.
We have not discussed the “Adjusted R-squared” in this class, but the rest of the output should make sense to you. Ask your TA if you have questions.
Question 3. What are the appropriate null and alternative hypotheses for the equivalent t-test of the regression slope?
Step 6: R reports a standard error for the population slope, β. Recall that the formula that we usually use: 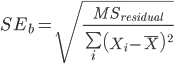 to calculate this standard error. Note, that by the definition of the variance we can rewrite the denominator as:
to calculate this standard error. Note, that by the definition of the variance we can rewrite the denominator as: 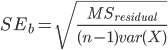 , R reports the “residual standard error” which is the square root of
, R reports the “residual standard error” which is the square root of 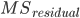 . Our sample size is n=15, so you should be able to calculate SE by dividing the number reported as the residual standard error by:
. Our sample size is n=15, so you should be able to calculate SE by dividing the number reported as the residual standard error by:
sqrt(14*var(data$months.driving)) ;
Question 4. What is the 95% CI for β ? (recall that you can get the t statistic that we use for the 95% CI from R with the command:
qt(.975, df=13)
Question 5. What is the P-value reported by R for the regression slope using the t-test?
Question 6: What are your conclusions about the slope of the regression of posterior hippocampus volume on months as a taxi driver?
Question 7. What proportion of the variation in posterior hippocampus volume is explained by the number of months driving a taxi?
Step 7: After we have fit a linear regression model to our data (as we did above), R makes it easy to generate a residual plot. Execute:
plot(resid(lin.mod) ~ data$months.driving,
xlab="months driving",
ylab="post.hippo residual (cu. mm)");
abline(h=0);
Does this plot make you question whether a linear model is a good fit for these data?
Step 7: Repeat the steps for creating scatterplots and linear regression for the anterior hippocampus.
Question 8. Based on this scatterplot, do you think that we will find a significant linear relationship between the size of the anterior hippocampus and the number of months spent as a taxi driver? Is the relationship positive or negative? Now, following the same procedure as above, use R to carry out regression analysis for the anterior portion of the hippocampus. Question 9. Write out the prediction equation for this regression analysis. What is the point estimate of the slope (b)? What is the point estimate of the y-intercept (a)?
Question 10. Are the results for the anterior hippocampus similar to what was found earlier for the posterior hippocampus? What is the P-value for this comparis?
PART 2. Correlation analysis
The correlation coefficient measures the tendency of two numerical variables to change together. We will briefly use R to calculate sample correlation coefficients (r) for our data, and to carry out hypothesis tests to test the null hypothesis that the population correlation coefficients (ρ) are zero.
Step 8: To get the point estimate of the correlation coefficient for the months as a cab driver and the posterior hippocampus measurements,, you can use:
cor(data$months.driving, data$post.hippo.diff) ;
Would you have obtained a different answer if you executed:
cor(data$post.hippo.diff, data$months.driving) ;
Step 9: To conduct a hypothesis test that the true correlation is 0, simply use:
cor.test(data$months.driving, data$post.hippo.diff) ;
Question 11. What is the P-value?
Step 10: We will now calculate the test statistic by hand. First calculate: 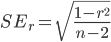 and then calculate
and then calculate 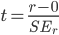 .
.
Question 12. What is the value of your test statistic? Does it agree with the value reported by R?
Question 13. What is the estimated correlation coefficient for the anterior hippocampus and months as taxi driver? What is the P-value reported by R?
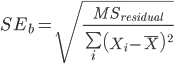 to calculate this standard error. Note, that by the definition of the variance we can rewrite the denominator as:
to calculate this standard error. Note, that by the definition of the variance we can rewrite the denominator as: 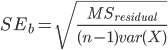 , R reports the “residual standard error” which is the square root of
, R reports the “residual standard error” which is the square root of 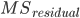 . Our sample size is n=15, so you should be able to calculate SE by dividing the number reported as the residual standard error by:
. Our sample size is n=15, so you should be able to calculate SE by dividing the number reported as the residual standard error by: